Impedance and Admittance

Impedance and Admittance


In the preceding section, we obtained the voltage-current relations for the three passive elements as

V = RI, V = jωLI, V = I/ jωC


These equations may be written in terms of the ratio of the phasor voltage to the phasor current as

 V/I = R, V/I = jωL, V/I = 1/jωC

From these three expressions, we obtain Ohm’s law in phasor form for any type of element as

Z =V/ I or V = ZI

where Z is a frequency-dependent quantity known as impedance, mea- sured in ohms.

>The impedance Z of a circuit is the ratio of the phasor voltage V to the phasor current I, measured in ohms.

>The admittance Y is the reciprocal of impedance,measured in siemens (S).

The admittance Y of an element (or a circuit) is the ratio of the phasor current through it to the phasor voltage across it, or Y =1/Z = I/V

EXAMPLE :

Insight Learning:

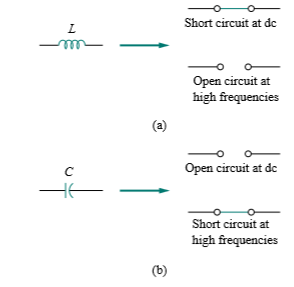
The impedance Z of a circuit is the ratio of the phasor voltage across it to the phasor current through it: Z = V I = R(ω)+jX(ω) The admittance Y is the reciprocal of impedance: Z = 1 Y = G(ω)+jB(ω) Impedances are combined in series or in parallel the same way as resistances in series or parallel; that is, impedances in series add while admittances in parallel add.