Sinusoids
> A sinusoid is a signal that has the form of the sine or cosine function.
A sinusoidal current is usually referred to as alternating current (ac). Such a current reverses at regular time intervals and has alternately positive and negative values. Circuits driven by sinusoidal current or voltage sources are called ac circuits.
Consider the sinusoidal voltage
v(t)= Vm sinωt
where
Vm = the amplitude of the sinusoid
ω = the angular frequency in radians/s
ωt = the argument of the sinusoid
It is evident that the sinusoid repeats itself every T seconds; thus, T is called the period of the sinusoid.
T =2π / ω
The fact that v(t) repeats itself every T seconds is shown by replacing t by t +T
v(t +T)= v(t)
that is, v has the same value at t +T as it does at t and v(t) is said to be periodic. In general,
>A periodic function is one that satisfies f(t)=f(t+nT),for all t and for all integers n.
As mentioned, the period T of the periodic function is the time of one complete cycle or the number of seconds per cycle. The reciprocal of this quantity is the number of cycles per second, known as the cyclic frequency f of the sinusoid. Thus,
Sinusoids are easily expressed in terms of phasors, which are more con- venient to work with than sine and cosine functions.
>A phasor is a complex number that represents the amplitude and phase of a sinusoid.
Phasors provide a simple means of analyzing linear circuits excited by sinusoidal sources; solutions of such circuits would be intractable other- wise. The notion of solving ac circuits using phasors was first introduced by Charles Steinmetz in 1893. Before we completely define phasors and apply them to circuit analysis, we need to be thoroughly familiar with complex numbers.
A complex number z can be written in rectangular form as
z = x +jy
where j = √−1; x is the real part of z; y is the imaginary part of z. In this context, the variables x and y do not represent a location as in two-dimensional vector analysis but rather the real and imaginary parts of z in the complex plane. Nevertheless, we note that there are some resemblances between manipulating complex numbers and manipulating two-dimensional vectors.
The complex number z can also be written in polar or exponential form as z = r φ = rejφ (9.14b) where r is the magnitude of z, and φ is the phase of z. We notice that z can be represented in three ways:
z = x +jy Rectangular form
z = r φ Polar form
z = rejφ Exponential form
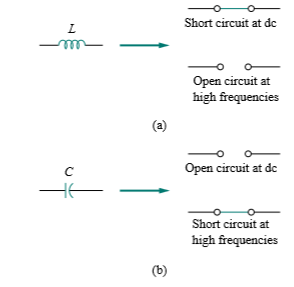
This shows that the derivative v(t) is transformed to the phasor domain as jωV
dv/dt (Time domain) ⇐⇒ jωV (Phasor domain)
Similarly, the integral of v(t) is transformed to the phasor domain as V/jω
Sv dt (Time domain) ⇐⇒ V/jω (Phasor domain)
Insight Learning:
A sinusoid is a signal in the form of the sine or cosine function. It has the general form v(t)= Vm cos(ωt +φ) where Vm is the amplitude, ω = 2πf is the angular frequency, (ωt +φ) is the argument, and φ is the phase.
A phasor is a complex quantity that represents both the magnitude and the phase of a sinusoid. Given the sinusoid v(t)= Vm cos(ωt +φ), its phasor V is V = Vm φ
In ac circuits, voltage and current phasors always have a fixed relation to one another at any moment of time. If v(t)= Vm cos(ωt +φv) represents the voltage through an element and i(t)= Im cos(ωt +φi) represents the current through the element, then φi = φv if the element is a resistor, φi leads φv by 90◦ if the element is a capacitor, and φi lags φv by 90◦ if the element is an inductor.